
数学では直感を裏切るような結論を導くことがあります.
特に「確率」に関する問題は,確率自体が目に見える量ではない一方で日常生活で何気なく使う概念であるため,直感と論理が一致しないことがあります.
確率の問題の中でも全米を熱狂させた「Monty Hall問題」を本記事で紹介します.
本記事を読むと日常生活で数学を使うと正しい結論を出す訓練になり,本質を見抜くヒントも書きました.
こんな人におすすめ
高校で学ぶ数学を前提に本記事を書きました.「条件付き確率」が必須の知識になります.
確率論を復習されたい方は,体系立てて書かれており説明もわかりやすい次の本がおすすめです.
Monty Hall問題
「Monty Hall問題」は,AmericaのTV game番組「Let's make a deal」の司会者Monty Hallに由来する,有名な確率puzzleです.
出典:Towards Data Science Let’s Make a Deal
直感を信じると間違える一方で,理論的に導き出された答えも何となく矛盾しているような気分になる不思議な問題です.
Monty Hall問題とは
Monty Hall問題
あなたは今,TV番組のgame showに参加しています.
Gameの規則は,次の通りです.
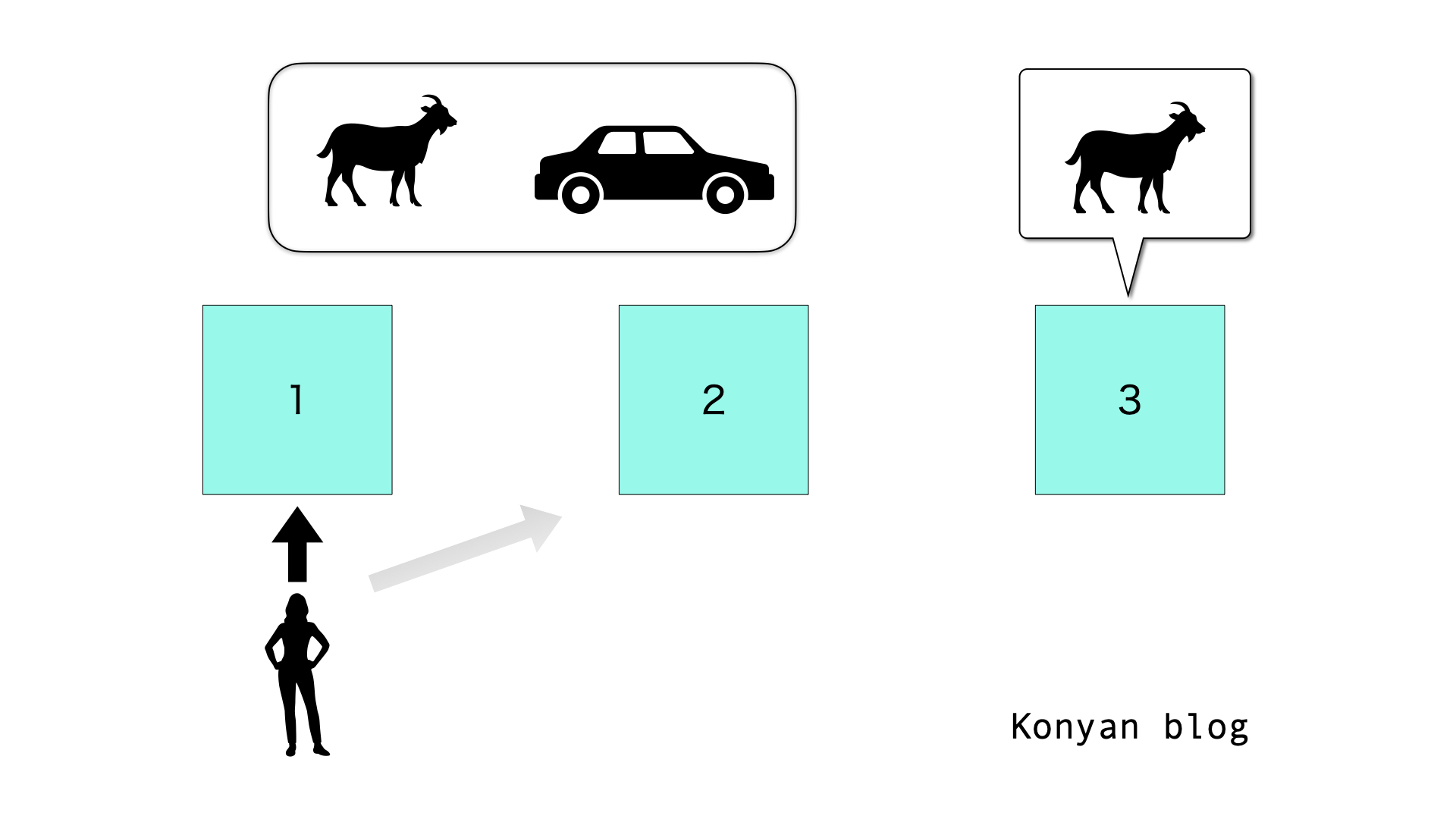
目の前に3つの扉があり,あなたには扉の向こう側が見えません.
扉の向こう側には,新車が1台とヤギ2匹がそれぞれ準備されています.
司会者は,どの扉の奥に何が隠されているかを知っていますが,あなたは知りません.
あなたは,直感的に扉 1を選びます.
答えを知っている司会者は不敵な笑みを浮かべて,扉3を開けて見せると,扉 3の向こうには1匹のヤギがいます.
司会者はあなたの心を見透かしたように言います.
「最後にもう一度選択する権利をあなたにあげましょう.扉 1を選びますか?それとも扉2に変更しますか?」
はじめに選んだ扉 1が”当り”の確率は\(\frac{1}{3}\).
同じように,扉 2が”当り”の確率も\(\frac{1}{3}\).

むしろ,司会者の人が”外れ”の扉に誘導している罠ではないかと勘ぐります.

司会者が扉 3を開けて”外れ”であることを見せたことにより,扉2が”当り”の確率は\(\frac{2}{3}\)になります.
よって,扉2に変更した方が”当り”になる確率が2倍になります.

司会者は,ただ”外れ”の扉がどれかを事後的に示しただけなのに,”当り”の確率が変わるなんて信じられない.

質問者さんのように,考えるようにうまく問題設定がされています.
問題の本質を見抜くために肝心なことは,
ポイント
あなたが選ばなかった,2つの扉どちらかに”当り”がある確率は\(\frac{2}{3}\)である.
今回は扉2が司会者によって”外れ”であることを示されましたが,平行世界では扉3が司会者によって選ばれていたかもしれない.
全米で1万人以上が熱狂
1990年当時,Monty Hall問題は物議を醸し出しました.
博士課程取得者1千人を含めた,1万人読者がMonty Hall問題の解法を取り上げた雑誌に反対意見を投稿しています.
確率論は,”起こりうる事象の発生頻度”を教えてくれますが,具体的に確率は目に見えるわけではないので,どうしても直感と理性が対立してしまいます.
一般化されたMonty Hall問題


ポイント
一般化することで,個別の事象よりも問題に対する見通しが良くなります.
Monty Hall問題が人を迷わせる”罠”は,3という数字です.
- あなたが選ぶ扉は1つ
- 司会者が”外れ”を見せる扉も1つ
- 最後にあなたが選ばなかった扉も1つ
全ての扉が対等に扱えるような気がしてくる点が,Monty Hall問題を長い間人々の間で論争を巻き起こした源流でしょう.
3の”罠”から脱出するために,次のような一般化されたMonty Hall問題を定式化します.
一般化されたMonty Hall問題 (D. L. Ferguson, 1970)
あなたは今,TV番組のgame showに参加しています.
Gameの規則は,次の通りです.
目の前に\(N\)個の扉があり,あなたには扉の向こう側が見えません.(\(N\)は3以上の任意の自然数とします.)
扉の向こう側には,新車が1台とヤギ\((N-1)\)匹がそれぞれ準備されています.
司会者は,どの扉の奥に何が隠されているかを知っていますが,あなたは知りません.
あなたは,直感的に扉 1を選びます.
答えを知っている司会者は不敵な笑みを浮かべて,あなたの選んだ扉 1とある扉\(i\)以外の,\((N-2)\)個の扉を開けて見せると,その扉の向こうには\((N-2)\)匹のヤギがいます.
司会者はあなたの心を見透かしたように言います.
「最後にもう一度選択する権利をあなたにあげましょう.扉 1を選びますか?それとも扉 \(i\)に変更しますか?」
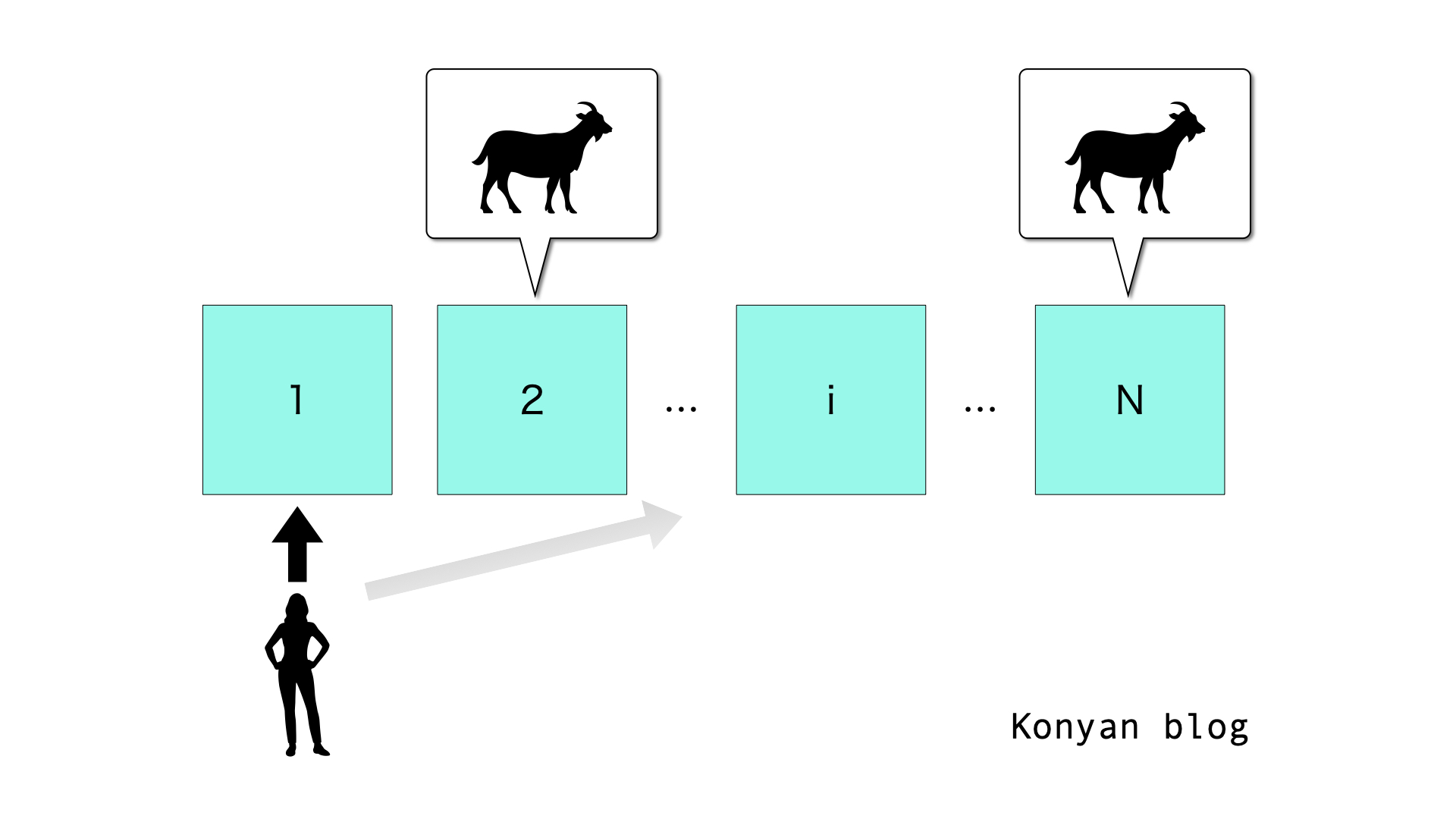
一般化すると,扉 1から扉 \(i\)に変更した方が良いことが直感でも分かります.
分かりづらい時は,\(N\)に大きな具体的な数字を当てはめてみてください.
ポイント
- あなたが選んだ扉 1が”当り”の確率は\(\frac{1}{N}\).
- あなたが選ばなかった\((N-1)\)個の扉に”当り”がある確率は,\(\frac{N-1}{N}\).
- 司会者は,扉 1以外の中からある扉を(意図的に)選んで,”外れ”であることを示した.つまり,\((N-1)\)個の扉に”当り”がある確率\(\frac{N-1}{N}\)が残された1つの扉に集約された.

扉 1に”当り”がある確率は\(\frac{1}{N}\).
一方で,司会者が残したもう一つの扉に”当り”がある確率は,\(\frac{N-1}{N}\).
したがって,扉 1からもう一つの扉に変更した方が合理的で,"当り"の確率は\((N-1)\)倍になる.
まさに一般化することで,枝葉末節に惑わされずに,回答の道筋を見つけることができました.
一般化というと小難しく聞こえますが,物事の本質を抽出するために,数学ではよく使う手法です.
数学の理論の中には,「一般化のための一般化」なんて野次をされて,一般化が目的になっていると批判されることもあります.
筋の良い一般化は大歓迎です!皆さんも日常生活で困ったことがあれば,悩みを俯瞰する方法として活用してみてください.
メモ
昔数学の先生が,「問題が押してダメなら,引いてみろ」と格言を残しました.
生徒の一人が,「どのように引くのですか?」と聞くと,「分からない」と先生は答えて教室中が爆笑の渦になりました.
一般化されたMonty Hall問題の解法
条件付き確率とBayesの定理を用いて解説します.
詳しくは次の記事をご参考ください.
-

-
【確率論】検査は本当に有効?なぜ何回も検査を行うの?Bayesの定理で数学的に考察してみた
続きを見る
記号を導入します.
\(A_{i}\) : 扉 \({i}\)が"当り"である事象(\(i=1,\dots,N\))
\(\overline{A_{i}}\) : 扉 \({i}\)が"外れ"である事象(\(i=1,\dots,N\))
\(B_{i}\) : 扉 1と扉 \(i\)以外の,\((N-2)\)個の扉が”外れ”である事象(\(i=2,\dots,N\))
すぐに次のことが導かれます.
$$P(A_{i}) = \frac{1}{N}$$
$$B_{i} = A_{1} \cup A_{i}$$
「あなたの選んだ扉 1とある扉以外の,\((N-2)\)個の”外れ”の扉を開ける」事象\(B\)は,次のように表せます.
$$B = \displaystyle\bigcup_{i=2}^{N} B_{i}$$
\(P(B)=1\)であることに注意してください.
Bayesの定理より,事象\(B\)が発生した条件下での事象\(A_{1}\)の確率は,
$$P(A_{1}| B) = P(A_{1}\cap B) = P\left(\displaystyle\bigcup_{i=2}^{N} A_{1}\cap B_{i}\right) = P(A_{1}) = \frac{1}{N}$$.
事象\(B\)が発生した条件下での事象\(\overline{A_{1}}\)の確率(扉 1でない方の扉が"当り"である確率)は,
$$P\left(\overline{A_{1}}| B\right) = P\left(A_{1}\cap B\right) = 1 - P\left(A_{1}| B\right) = \frac{N-1}{N}$$.
まとめ:Monty Hall問題は条件付き確率で考える,一般化することで本質が見える
Monty Hall問題では,最初の選択からもう一つの選択に変更することで,”当り”の確率が2倍になることがわかりました.
もう一つ強調したいことは,Monty Hall問題を解く上で用いた「一般化」という方法です.
「もし,3つでなくて,たくさんの選択肢があった場合はどうなるんだろうか?」と視点をずらすことで,物事の見通しがグッと良くなります.
